
今回はフィボナッチ数列の実装をしてみたいと思います. フィボナッチ数列とは以下のように定義されます.

まず1つ目は再帰関数を使った実装です. 再帰関数とは処理の中で自身を呼び出す関数のことです. フィボナッチ数列の定義通りにフィボナッチ数列の第n項(n番目の数字)を求める関数を書いてみます.
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
for i in range(30):
print(fibonacci(i))
counter = 0
def fibonacci_count(n):
global counter
count += 1
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci_count(n-1) + fibonacci_count(n-2)
count_list = []
for i in range(36):
counter = 0
fibonacci_count(i)
count_list.append(counter)
print(i,counter)
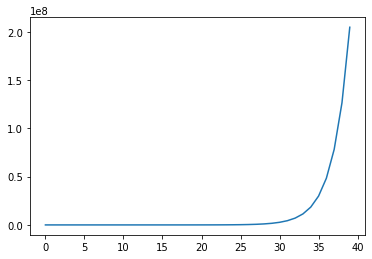
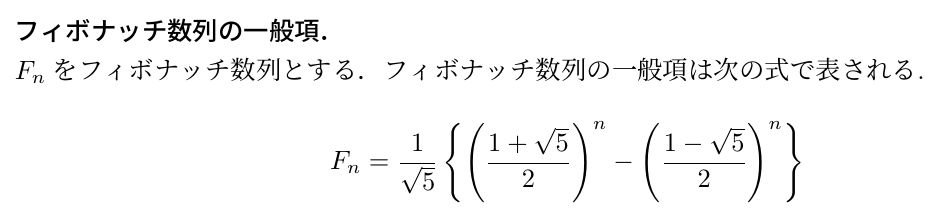
ところでフィボナッチ数列の一般項が出てきたときに,最初からこれを使って計算すればいいじゃないかと思った方はいませんか? 私もそう思います.一般項を使ってフィボナッチ数列を求める関数を作りました.
def fib_general(n):
fib = (1/(5**0.5)) * (((1+(5**0.5))/2)**n - ((1-(5**0.5))/2)**n)
return int(fib)
for i in range(101):
print(i,fib_general(i))
気を取り直して次の解決策を探りましょう. 再帰関数の抱える問題はnが増えるにつれて関数を呼び出す回数が増えていくことが問題でした. より詳しく関数が何回呼び出されているのか調べてみましょう.
def fibonacci_count2(n):
global count_list
count_list[n] += 1
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci_count(n-1) + fibonacci_count(n-2)
count_list = [0 for i in range(21)]
fibonacci_count2(20)
for i in range(21):
print(i,count_list[i])
def fibonacci_list(n):
fib_list = [0 for i in range(n+1)]
fib_list[0] = 0
fib_list[1] = 1
for i in range(2,n+1):
fib_list[i] = fib_list[i-1] + fib_list[i-2]
return fib_list[n] # [n]を外せばフィボナッチ数列のリストを返すようにもできます
fibonacci_list(100)
リストを使う方法の敗因はリストを使い記憶容量を使い果たしてしまうからでした. 考え方として一度求めたものを計算せずに済ませるという方法は有効そうです. 何か他に手はないでしょうか? 小さいほうから順番に求めていけばわざわざリストで記憶せずとも計算ができます.
def fibonacci_step(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
a_0 = 0
a_1 = 1
for i in range(n-1):
a_2 = a_0 + a_1
a_0 = a_1
a_1 = a_2
return a_2
fibonacci_step(1000000)
今回は4通りの方法を使ってフィボナッチ数列の計算をしてみました. コンピュータを使った数値計算をする場合に誤差に気を付けなければいけないこと,記憶容量に気を配らなければいけないことが 実感していただけたと思います.

# 行列の積の定義
def matrix_multi(A,B):
C_00 = A[0][0]*B[0][0] + A[0][1]*B[1][0]
C_01 = A[0][0]*B[0][1] + A[0][1]*B[1][1]
C_10 = A[1][0]*B[0][0] + A[1][1]*B[1][0]
C_11 = A[1][0]*B[0][1] + A[1][1]*B[1][1]
C = [[C_00,C_01],[C_10,C_11]]
return C
# 繰り返し2乗をする関数
def repeat_pow(A,n):
if n == 1:
return A
elif n%2 == 1:
B = repeat_pow(A,n-1)
return matrix_multi(A,B)
else:
A = repeat_pow(A,n/2)
return matrix_multi(A,A)
A = [[1,1],[1,0]]
print(repeat_pow(A,100)[0][1])